Abstract
The Heston stochastic volatility model explains volatility smile and skewness while the Black-Scholes model assumes a constant volatility. With the explicit option pricing formula derived by Heston, we use the Least Squares Fit to calibrate and do a robustness check as our back test. Then we do a case study of initial parameter to find out the influence of using different initial parameters. Therefore, we use moment matching to estimate a initial parameter. Using this method in the real market behavior, we can give recommendations on choosing initial parameters for stocks under different market behaviors
Robustness Check
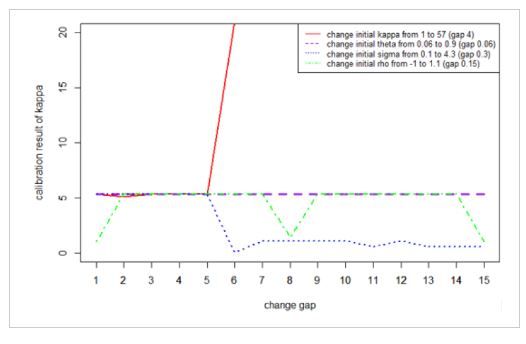
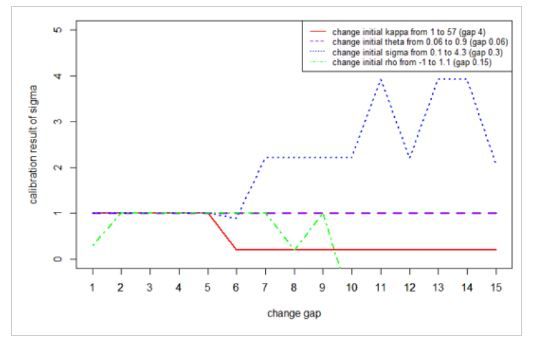
We check the robustness by trying different initial values in the least-square fit: $\min \sum_{i=1}^N (C_{mkt}(K_i, T_i)-C_{\Theta}(K_i, T_i))^2$, where $\Theta=\{\kappa, \theta, \sigma, \rho, v_0\}$ is the set of Heston parameters. From the figures we can see the cablibration result is sensitive to the initial points. Therefore we use moment matching to get a good initial point.
Researchers:
Research Group (2015 Spring):
Xingxian Zheng, Master in Financial Engineering, Graduated in May 2015
Wenting Zhao, Master in Financial Engineering, Graduated in May 2015
Advisor:
Dr. Ionut Florescu
Research Topics:
Heston model, calibration, moment matching
Main Results:
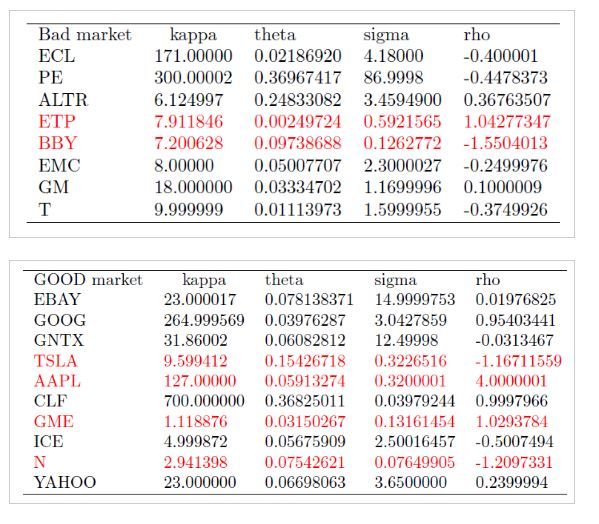
Calibration for different stocks under different market behaviors
As we know from the previous method and the importance of the initial parameter, we use the raw initial method in real market.
Conclusions
After getting the calibration result, we compare the results in different market behavior and give the recommendations on choosing the initial parameter.