Researchers:
Anthony Jonathan Riachi
Robert Leiser
Faculty advisor:
Cristian Homescu
Abstract:
In this paper we study different methods of dynamic hedging of options using machine learning techniques, specifically reinforcement learning techniques to find optimal hedging strategies in the presence of trading costs, discrete trading intervals and market frictions. We compared the Reinforcement Learning (RL) agents against a baseline Delta hedging agent on a European call option for a single underlying stock based on risk and cost performance. The agents were trained under option data simulated under log-normal and stochastic volatility processes. While the RL agent was able do as well as a delta agent with respect to the hedging risk, it outperformed the Delta agent when it came to reducing overall transaction costs for the same amount of risk.
Research in this project is focused on making covariance matrix robust- (exponentially weighted moving average (Himbert, Kapraun and Rudolf (2019)), linear shrinkage (Ledoit and Wolf (2003)), and de-noising (Lopez de Prado (2019)).) In this paper we test the performance of mean-variance portfolios with robust covariance over the previous 10 years.
Results:
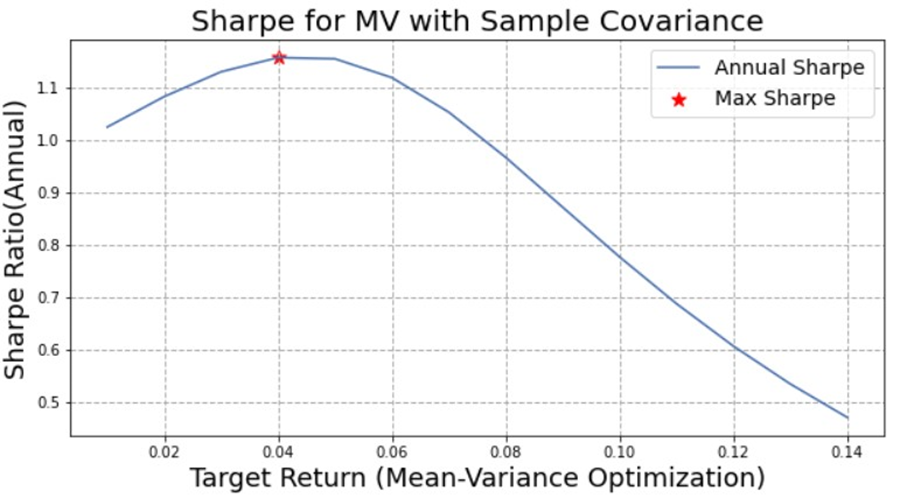
The paper provides the performance results and risk profiles of 11 different portfolio construction methods, including 5 mean-variance methods, 5 reward-risk parity methods, and 1 equal weight portfolio. The analysis looks at cumulative returns, year-on-year statistics and risk measures for each method, as well as estimation errors for mean-variance portfolios. The best "required return" for highest Sharpe ratio for mean-variance methods is also found.
The paper also provides annual statistics and risk measures for each mean-
variance allocation method over the past eleven years. There are annual statistics and risk measures for "Sample", "EWMA", "Shrunk", "Denoised", "Shrunk+Denoised".
The paper also ranks portfolio allocation methods based on risk measures.
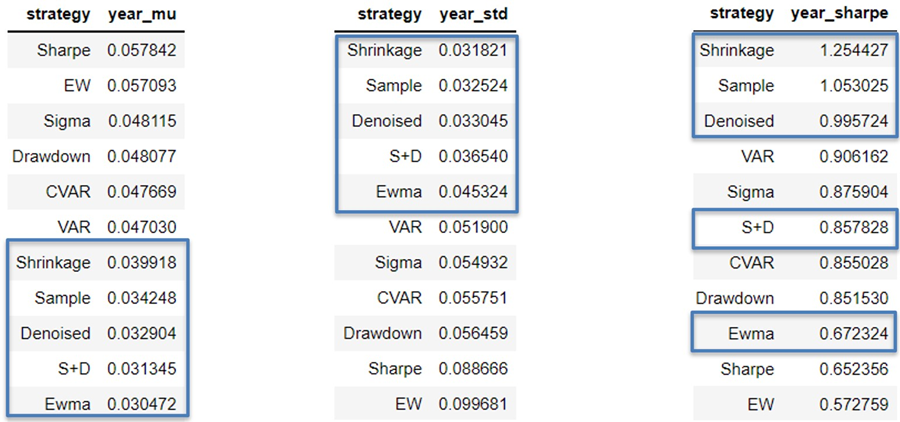

It estimates errors and compares them for the entire backtesting period. Sample had the highest estimated errors every year, followed by Denoised, Shrunk, and finally, Shrunk denoised with the smallest errors.
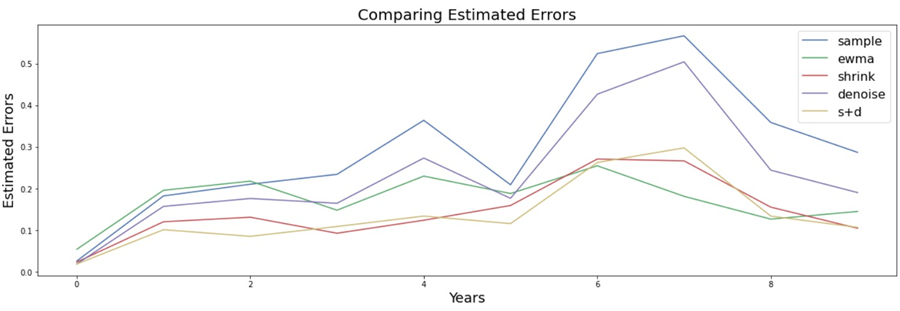
A testing is performed to determine which expected return (input in our optimizer) would yield portfolios with highest Sharpe ratio. We took two examples: mean-variance with linear shrinkage that yields 6 percent as the best input for our optimizer. And, mean-variance with sample covariance yields 4 percent.

This paper tests the performance of different portfolio allocation methods including mean-variance with sample and robust covariance matrix, reward-risk parity strategies and the equal weighted portfolio. These portfolios are evaluated based on their risk measures over a ten-year back testing period.
The process starts with selecting assets using maximum de-correlation and then computing expected returns, standard deviations, and covariance matrices. During high volatility market regimes, mean-variance portfolios outperformed other portfolios in terms of downside risk and Sharpe ratios, with "Shrunk" performing the best in terms of cumulative returns, standard deviation and Sharpe ratio, and "Shrunk + De-noised" performing the best in terms of maximum drawdown, VaR, and CVaR. "EWMA" was the worst performer among all portfolios.
Conclusion:
In conclusion, the mean-variance portfolio construction outperformed other methods in terms of risk management. The robustness of the different versions of the covariance matrices was also demonstrated by their lower estimation errors. The "Shrunk" and "Shrunk + Denoised" portfolios resulted in the lowest estimation errors, indicating that robust covariance matrices are effective in providing smaller changes in portfolio weights.