Researchers:
Mark-Jonathan Pabalan
Diyan Rahaman
Faculty Advisor:
Dr. Ionut Florescu
Abstract:
In this paper we study different methods of dynamic hedging of options using machine learning techniques, specifically reinforcement learning techniques to find optimal hedging strategies in the presence of trading costs, discrete trading intervals and market frictions. We compared the Reinforcement Learning (RL) agents against a baseline Delta hedging agent on a European call option for a single underlying stock based on risk and cost performance. The agents were trained under option data simulated under log-normal and stochastic volatility processes. While the RL agent was able do as well as a delta agent with respect to the hedging risk, it outperformed the Delta agent when it came to reducing overall transaction costs for the same amount of risk.
Results:
For the purposes of this project, we restricted our analysis to comparing a baseline Delta Hedging agent with an RL Agent using the Trust Region Policy Optimization (TRPO) algorithm trained on simulated data.
Training of the RL Agent was done over 200K episodes using stock price data for a single stock ticker AMZN using both a Geometric Brownian Motion model and a Heston model calibrated to historic data. The Environment was also setup to handle multiple transaction costs - 25, 50 and 75 bps (0.25%, 0.50% and 0.75%) of total volume transacted. The Agents were setup to re-balance every 1 day, 3 days and 6 days, which corresponds to a frequency of 90, 30 and 15 times for a 90-day European Call option on AMZN stock.
On a typical run we can see that the RL Agent was able to learn somewhere between 100K and 200K episodes. Once trained, when the RL agent was tested against a baseline Delta agent, we can see that it performs hedging actions that it learned from data were very close to the actions taken by a theoretical model:
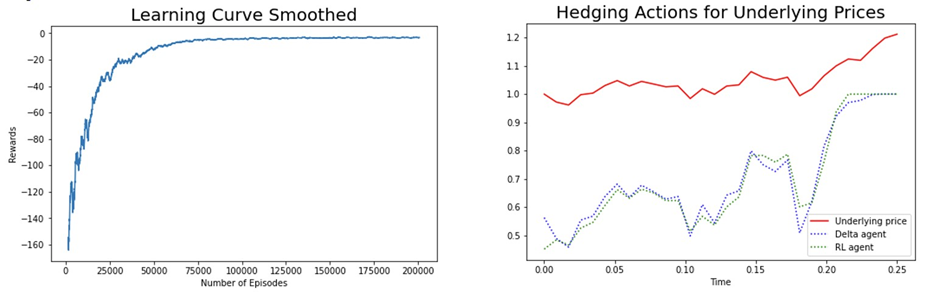
Figure 1: Training using a 90-day Call option simulated using GBM Model with 0.50% transaction costs and 3-day trading frequency
Validation testing was carried out over 10K randomly generated test samples and we can see how the Total P&L of each agent performed by comparing the Kernel Density Distribution of the t-statistic compared to 0. Looking at the Total Cost distribution of the RL Agent compared to the baseline Delta Agent we can see that the RL agent is able to maintain an overall lower cost:
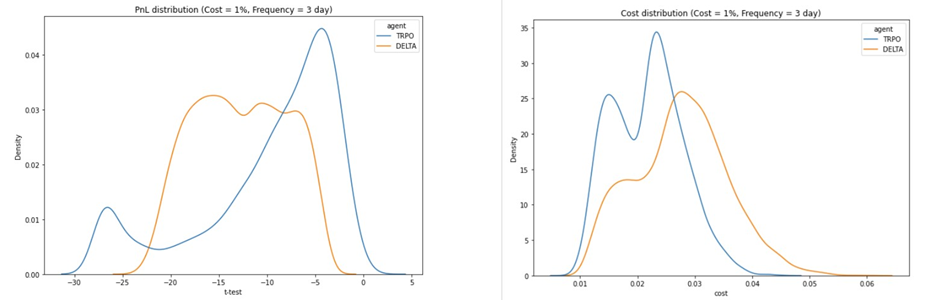
Figure 2: Validation testing using a 90-day Call option simulated using GBM Model with 0.50% transaction costs and 3-day trading frequency
Conclusion:
The RL Agent is able to perform almost as well as the Delta Agent in reducing the risk with small improvements under the RL Agent with respect to the VaR and CVaR. What’s more evident is that the RL Agent is able to reduce the total costs as transaction cost and frequency increase. As transaction costs increase, the Delta Agent is unable to account for the change in its calculations. However, our RL Agent utilises costs in order to make its hedging actions. This difference allows it to hedge more cost efficiently than the Delta Agent without sacrificing risk.
Overall, the RL agent is an improvement to the Delta Agent under VaR, CVaR, and Total Costs under realistic market conditions, all while hedging similarly with respect to the risk.
Lessons learned and future work:
RL Agents are very difficult to train, as they are very sensitive to the reward function. They are also very sensitive to the algorithm and hyper-parameters used, and requires a lot of trial and error to get the learning right. This tinkering process constituted for most of the early roadblocks in our timeline.
Data collection, especially locating large quantities of historic data for training, was also difficult. In order to acquire the required amount of option data for RL Agent training, a model simulation was used with the GBM and Heston models calibrated on actual data. This data of ample size take time to run and train. As a result, the selected option parameters and underlying asset studied were limited and the different types of RL Agents studied was also limited to a single TRPO model. In order to obtain more realistic results, more time could be allocated to historical data collection. Acquiring more option data and expanding the data sets could lead to more asset dynamics that could have been studied.
With the inclusion of more data, a better computing processor to run simulations and agent training would need to be established. Decreasing computing time and improving simulation speeds could have expanded our study of more varied option contract parameters for more insights: Put versus Call Options, Exotic Options, option portfolios based on multiple or single assets, etc. As a result, more work can be done to explore other Model-Free RL Methods to see how they compare with the baseline Delta Agent and find better hedging strategies.