Abstract
The aim of this study is to price VIX option by using stochastic volatility model with jumps. We build our model based on SVJJ model (Lian & Zhu, 2009). Parameters are calibrated using moment matching method, and we use Monte Carlo and Fast Fourier Transform as pricing methods. In the end, we put our model into use on empirical data.
Researchers:
Research Group (2016 Fall):
Pu Shi, Master in Financial Engineering, Graduated in Jan 2017
Yan Yu, Master in Financial Engineering, Graduated in Jan 2017
Mingdi Yao, Master in Financial Engineering, Graduated in Jan 2017
Advisor:
Dr. Zhenyu Cui
Dr. Thomas Lonon
Research Topics:
Option Pricing, Stochastic Volatility Model, SVJJ Model, Log-normal Jump Size
Main Results:
The historical data we use is VIX daily price. From there we calculate characteristic functions. For further study, it is logical to assume the jump size of underlying process is log-mix-norm distribution.
Conclusions
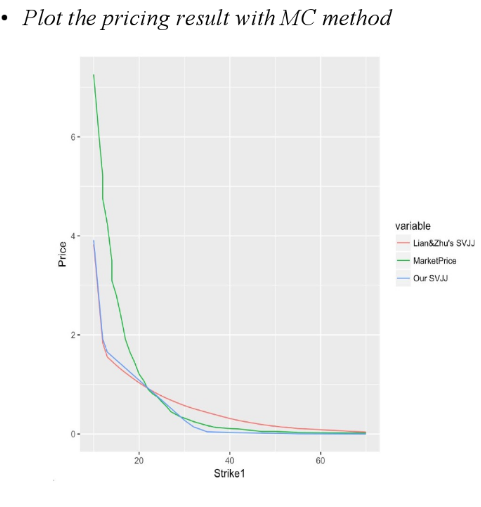
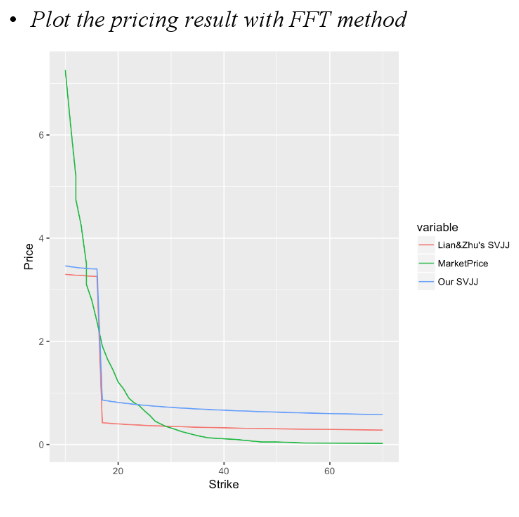
In this project, we build a SVJJ model based on Lian&Zhu's paper by changing the jump size at variance process from exponential to log-normal distribution. Our model outperforms Lian & Zhu's model under Monte Carlo pricing method, while under FFT pricing method, both models do not price call options closely. We should use different data sets in the future to calibrate the models to make it more accurate.