Hedging of Illiquid Assets Options with LSTM Neural Networks

Researcher

Yige Wang, M.S. in Financial Engineering, Graduated December 2019

Advisor:
Dr. Zhenyu Cui

Abstract

The hedging problem of illiquid asset options has long been a popular topic among academia. Classic models have been applied but suffer from their deficiency and constraints. In this report, we develop a model-free and data-driven methodology to solve hedging problems of illiquid assets with the help of LSTM neural networks. We investigate the initial endowment, the hedging strategy, and the distribution of hedging error for two different loss function, and discuss the influence of transaction costs.

Main Results

We first test the validity of our model using analytic solutions of the Heston-Nandi GARCH (HN-GARCH) model. The initial endowment $V(0, S(0))$ and hedging strategy $\Phi(0, S(0))$ will be justified and the distribution of total wealth change, i.e. the hedging error, will also be examined under different loss functions, and under conditions of with/without transaction costs.

Observations show that the discrepancy of the initial endowment $V_0$ and the hedging strategy $\Phi_0$ both remain less than 5%, which indicates the validity of our model.

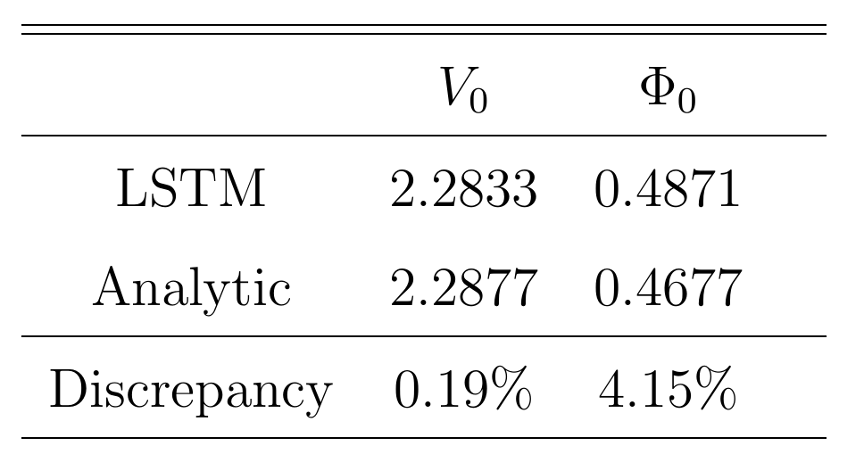
After the validation of our model, we could move on and testify the difference between different loss functions. Similar comparison is applied here, and we notice that both initial endowments are around $2.28, and the discrepancy of hedging strategies is slightly above 4%. Such results confirm that both loss functions are promising, and we would further investigate the difference between these two loss functions.

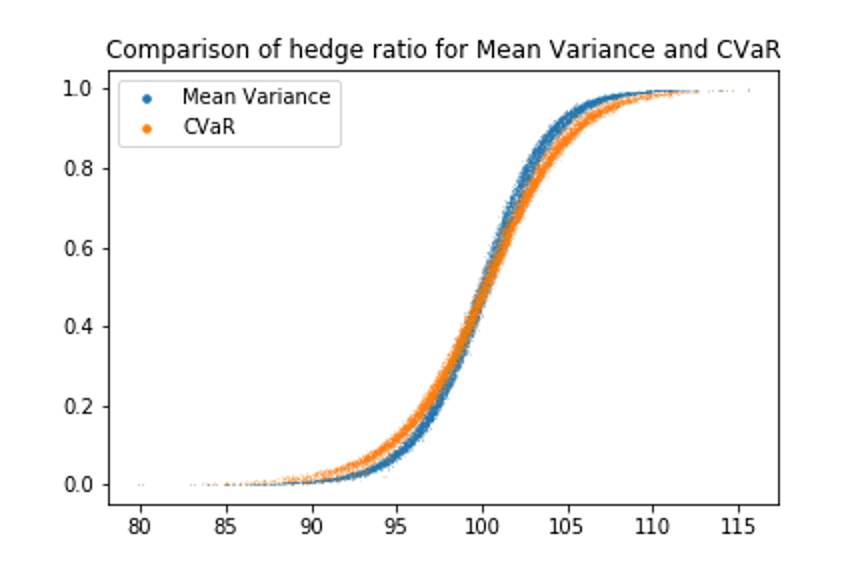
We compare the hedge ratios of two loss functions versus the change of underlying price at a snapshot of $t=20$ in Figure 1. Both two lines converge to 1.0 at deep in-the-money range, and get close to 0.0 within out-of-the-money regime. However, the curve of Mean Variance shows a slightly larger slope than that of the CVaR curve. Such pattern results from the feature of the CVaR loss function, that it concerns more about the distribution of the hedge error $\Delta W$, so that it is less sensitive to the change of underlying price itself.

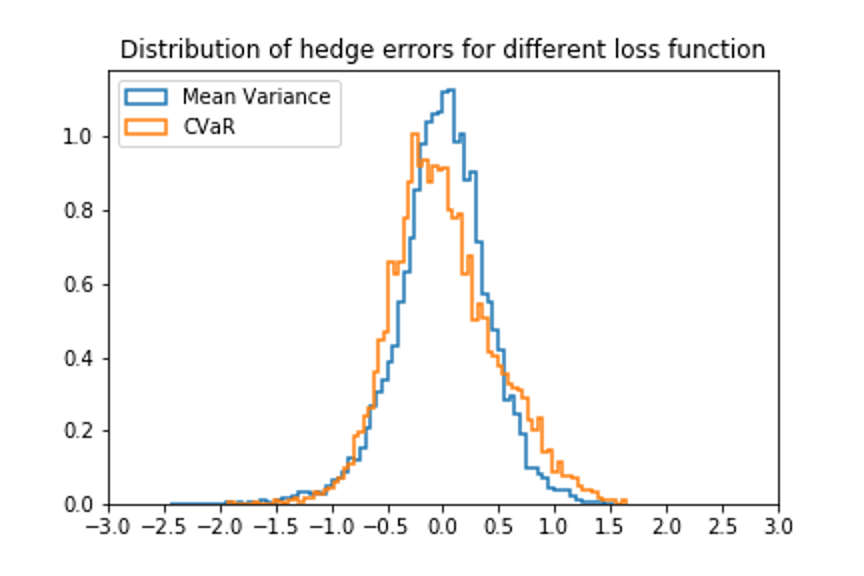
We move on to the investigation of the distribution of hedge error $\Delta W$ as displayed in Figure 2. More statistics are shown in Table 2, and it is obvious that the mean and variance for the mean variance loss function are smaller than their counterparts for the CVaR loss function. At the first glance, we might conclude from these statistics that the mean variance loss function outperforms CVaR. However, after a second thought, we realize that it is because the loss function is called ``mean variance", and the CVaR loss function should be reasonable or even more practical because it concerns more about the tail of the distribution. As shown in Figure 2, the distribution for CVaR actually has a short tail than the mean variance loss function. In this case, we shall not say that one of the loss functions is better than the other. Instead, both of these loss functions have their advantages in relevant fields. The mean variance loss function might be utilized more by traders, because they care more about the expectation of their investments, while risk managers might prefer the CVaR loss function because their concern how much money they might lose in the worst case.

After the comparison between two loss functions, we move on to testify the impact of transaction costs. In our project, we implied a proportional transaction cost of 0.2%, and investigate its influence on the initial endowment $V_0$, hedging strategy $\Phi_0$, and the distribution of hedging error $\Delta W$.

Conclusion

In this report, we successfully developed a model-free / data-driven methodology to solve hedging problems of illiquid assets using LSTM neural networks. We investigated the initial endowment, the hedging strategy, and the distribution of hedging error for two different loss functions, and discussed the influence of transaction costs. We conclude that both of the two loss functions are valid and efficient, while they both have their own priorities and usefulness. We also confirm that the presence of transaction costs will result in an increase of final option price, while the hedging strategy and hedging error remain unchanged. The biggest advantage of our model is that it does not require any pre-defined model or assumes any restriction of dataset. Simply put modified data into our model and a justified result will be provided. Such capability is valid for all kinds of data under discrete-time context. Further researches might be extended on topics about the influence of different hedging frequencies, or the impact of different option types, such as binary options, or target volatility options.