Abstract
The aim of this project is to present evidence that exchange rates can be modeled by a jump-diffusion process, where the jump component is a log mixture of normals. We demonstrate that the model is a reliable approach for pricing foreign exchange options. We also derive an analytic solution for the price of a European foreign exchange option. The developed algorithms show the potential use of the model for evaluating other exchange rate derivatives.
This paper presents a jump-diffusion model with a Log Mixture of Normals jump component for pricing exchange rate derivatives. This model for pricing European foreign exchange options is based on the one given in (Merton, 1976) as:

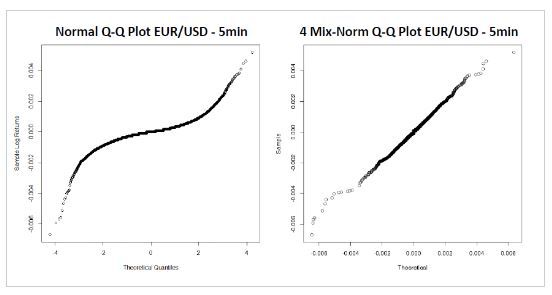
Jump diffusion models are proposed to address the leptokurtic behavior. We can see that by having a mixture-normal distribution as the jump size distribution, we improve the fit of our model. This gives a strong evidence that the log returns of this 5-minute data is drawn from a mixture of four-normal distributions.
Researchers:
Research Group (2015 Fall):
Nikolay Radev, Master in Financial Engineering, Graduated in Jan. 2016
Advisor:
Dr. Thomas Lonon
Research Topics:
Jump-Diffusion model, Exchange Rate Options, Estimation Maximization Algorithm, Option Pricing
Main Results:
As an example, we take a look at the spot exchange rate GBP/USD from April 9, 2015 to October 9, 2015, at 5-minute time intervals. Assuming that the log returns are distributed according to a mixture of 3 normals, the EM algorithm is used to determine the parameters of the mix-normal distribution. We use the Q-Q plot (Figure 2) as evidence that mixture of 3 normals is a better t for the market data compared to one with a single normal distribution.

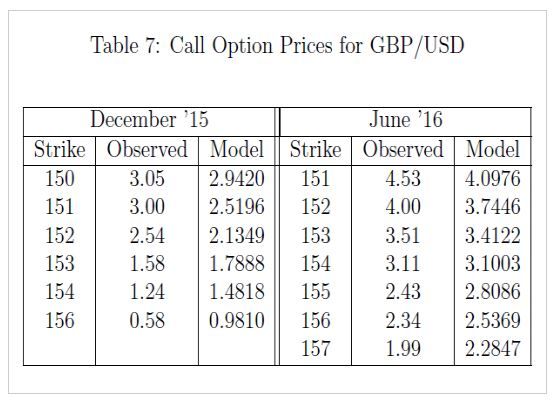
Tables 7 presents the call option prices obtained by the model in U.S. dollars, alongside the observed prices, for various maturities. The specific maturities are selected, because of relative completeness of the option chains associated with them. The closing spot exchange rate on October 9, 2015 for EUR/USD was 1.5307, the 1-year risk-free interest rate in U.S. dollars was 0.239% and 0.506% in British Pound.
Conclusions
Our pricing model developed in this project has successfully captured the momentum of the foreign exchange options. As can be seen from the table above, it has stayed closely with the observed data. A constant term may be added to the predicted option price to fit the observed data better. This can help us in many ways that, we can use our model to price the options and profit from trading it.