Researchers:
Gordon Garisch
Faculty Advisor:
Dr. Zachary Feinstein
Abstract:
This project uses a measure of systemic risk to determine the allocation of additional capital in a financial network. Using an Eisenberg-Noe framework, several machine learning models and simulation procedures are proposed for efficient and acceptable capital allocations. Logistic regression with various kernel specifications and basic neural networks are explored for accuracy and computational efficiency.
The impact of using Gibbs sampling in capital allocation simulation is also examined. The methodology is applied to a dataset of European banks, and it is found that basic neural networks provide more accurate and computationally efficient capital allocations than logistic regression with various kernel specifications.
Results:
This project results in 2-5 dimensions using two sampling methods.
ES simulation-
In ES simulation, 100 external inflow samples are used for each iteration to determine if the system is under stress.
Gibbs sampling-
In Gibbs sampling, at least 30 marginal samples iterations are performed, increasing with dimensions.
Sampling iterations-
Sampling iterations for this project are 100, starting with 25 samples and adding 25 samples (uniformly distributed and through Gibbs sampling) at each iteration.
With these parameters and considerations explained we can review the results of the analysis.
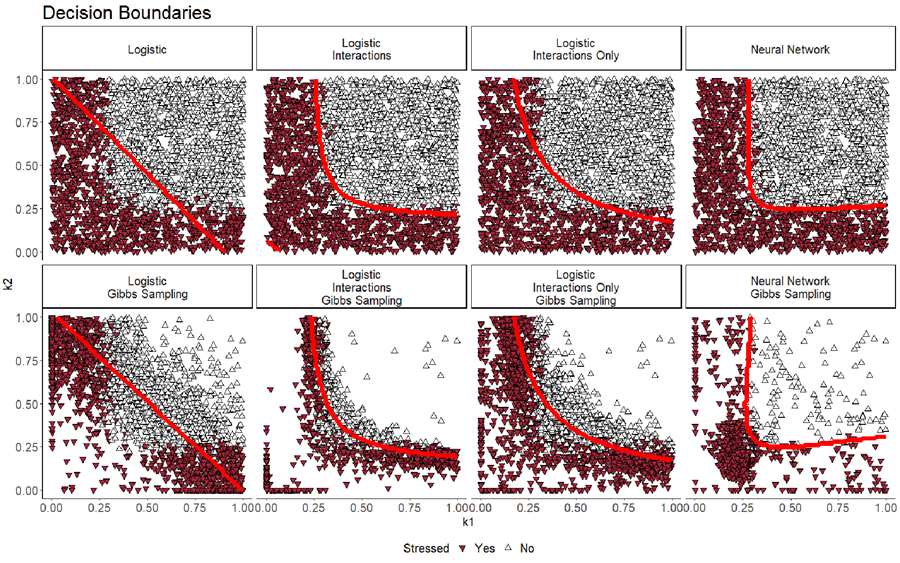
In pure random sampling, there may be a situation where both capital levels are close to zero, and a boundary is introduced around that area. However, this boundary placement is not logically sound and may cause issues in larger dimensions. Therefore, this approach is not considered a robust model.
However, this issue does not seem to affect the models created using Gibbs sampling.
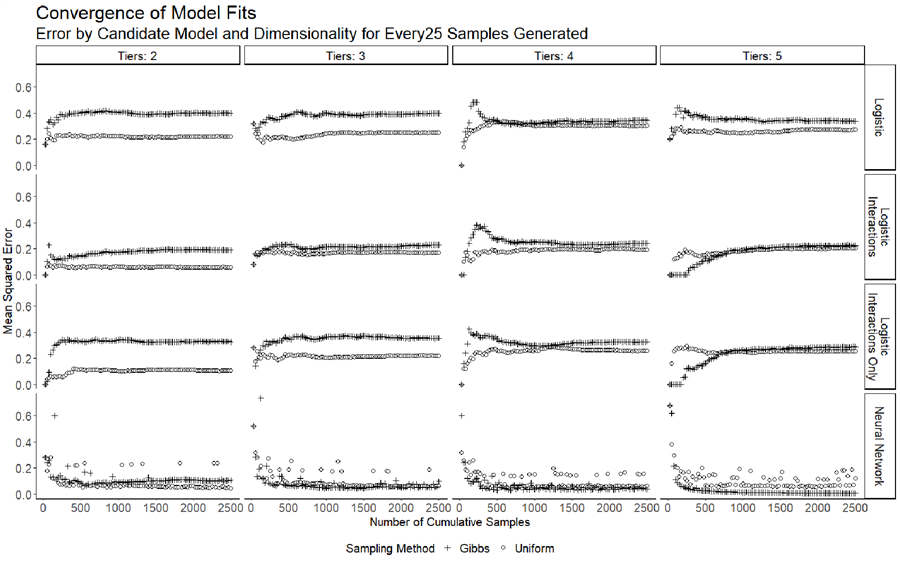
Gibbs sampling works faster and neural network models perform the best in this project. Logistic regression models that include interactions also work well. Losses increase slightly as the number of dimensions increase, but not exponentially or linearly. This means that the method can handle an increase in dimensions well.
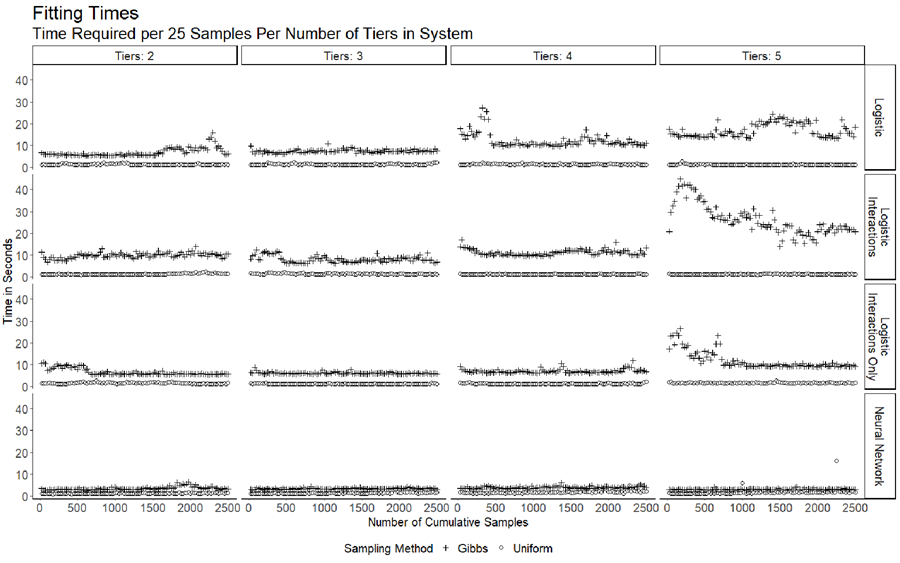
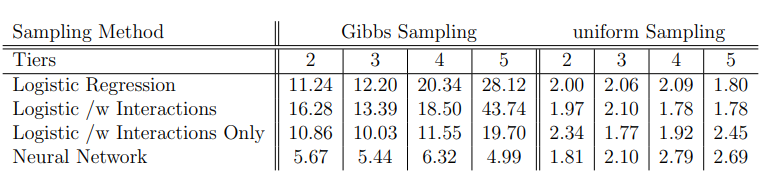
The table provides a view of the total execution time. It discusses the relative resource intensity of Gibbs sampling and generating random samples, as well as the execution times of logistic regression with different kernels and their relationship with data dimensionality.
It suggests that Gibbs sampling is more resource-intensive than generating random samples, and complex kernel logistic regression has longer execution times than linear kernel logistic regression or neural networks, and these times increase more quickly with increasing data dimensionality.
The instances of neural networks used in this project show the best execution times of all candidate models, and has a much smaller multiple of execution times of Gibbs sampling vs. uniform sampling than the logistic regression models. This may be due to enhanced implementation procedures, or due to the hyperparameters utilized for these particular models.
Conclusion:
This project successfully develops machine learning models to measure systemic risk in a simplified capital allocation system for a network of 87 banks. Neural networks are identified as the most accurate and efficient model, while logistic regression with various kernels presents issues with poor fits, longer execution times, and potential monotonicity problems.
The use of Gibbs sampling improves convergence but reduces accuracy. Non-parametric approaches, such as Gaussian regression, may provide a more consistent framework for higher dimensions. Future work could explore improved algorithms for dealing with exploding gradients and monotonicity, as well as improving code efficiency.