Abstract
In this project, we analyze stock prices movement after shocks have appeared. We explore the reaction of financial markets to shocks using a modified model of market dynamics with price expectations resemble to a damped harmonic oscillator model. In order to do this, we gather data from indices of a variety of financial markets such as NYSE and NASDAQ. We establish the amount by which each market felt the shocks, a dampening factor which expresses the capacity of a market of absorbing a shock, and also a frequency related with volatility after the shock. The other model focused in this paper is polynomial regression model. After the predictions of stock values, we made a portfolio to compare between these models.
Researchers:
Research Group (2015 Fall):
Pushkar Sagdeo, Master in Financial Engineering, Graduated in Jan. 2016
Ketan Mali, Master in Financial Engineering, Graduated in Jan. 2016
Advisor:
Dr. David Starer
Research Topics:
damped harmonic oscillator, polynomial regression, shocks
Main Results:
We establish the equation $x(t)=k+Ae^{-\alpha t} \cos (\omega (t) + \phi)$ , where $t$ is a future time in minutes, $x(t)$ is the predicted stock price, $k$ is the steady stock price, $\alpha$ is decay rate, $\omega$ is oscillator frequency, $A$ is jump between stock prices and $\phi$ is angular frequency. We applied Damped Harmonic Oscillator Model on 12 different stock companies to predict stock values for the next 4-6 minutes. The results are as expected, the majority of predictions are quite in the same direction as actual stock value. Out of 12 companies, our prediction was quite accurate for 7 companies. This means that there are more chances of getting a profit after selling stock at the predicted time and predicted value. The figures show the training data and the predicted value for 4 stocks out of 12.
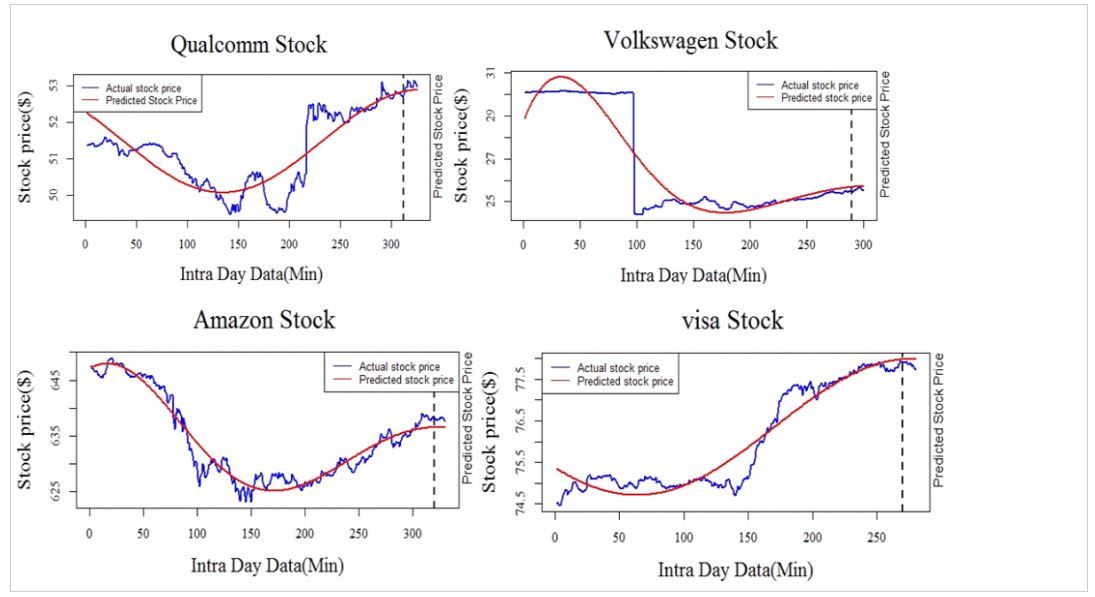
Polynomial Regression Model
We use a third-order equation: $x(t) = a_0 + a_1t + a_2 t^2 + a_3t^3$ where $a_0, a_1, a_2, a_3$ are changing parameters depending upon stock price. Out of 12 companies, our prediction was quite accurate for 3 stocks and for the rest of stocks, the model was not predicting as per stock price. Here are some figures showing the training data and the predicted value.
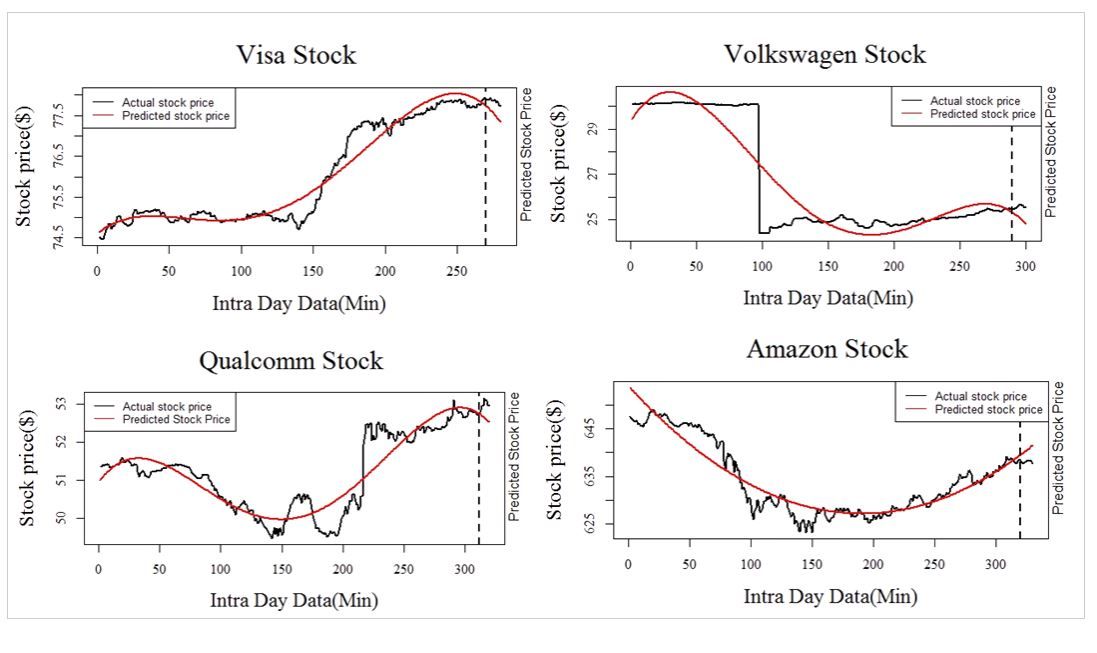
Portfolio
Based on the predicting results we construct investment portfolios using the 12 stocks under the two models. The table below makes a comparison between the two portfolios.

Conclusions
Our predictions on stock prices using the Damped Harmonic Oscillator Model are pretty accurate for the short period after the shock. On the other hand, the Polynomial Regression model does not work as well as the former. Hence in this study, we have achieved our original goal, which is to find better model in predicting stock movements after a shock has occurred.