Researchers:
Zhuofan Li
Faculty Advisor:
Dr. Zachary Feinstein
Abstract:
This paper discusses systemic risk in the financial system, which refers to the risk associated with any part of the system that could cause the entire system to collapse or fail. This paper proposes an efficient algorithm to measure systemic risk in order to prevent such failures. Financial regulators require individual institutions to allocate additional capital to avoid default and prevent system failure. However, standard algorithms such as Value at Risk and Expected Shortfall are not effective for larger systems. The author presents an algorithm that can compute and apply systemic risk measurements to solve the issue of dimensionality.
Methodology:
The idea of the method is to classify the outcome caused by the additional capital allocation into two groups: satisfying the requirement and not satisfying the requirement. Hence the systemic risk measures can then be approximated by the classification boundary.
2.1 Logistic Regression:
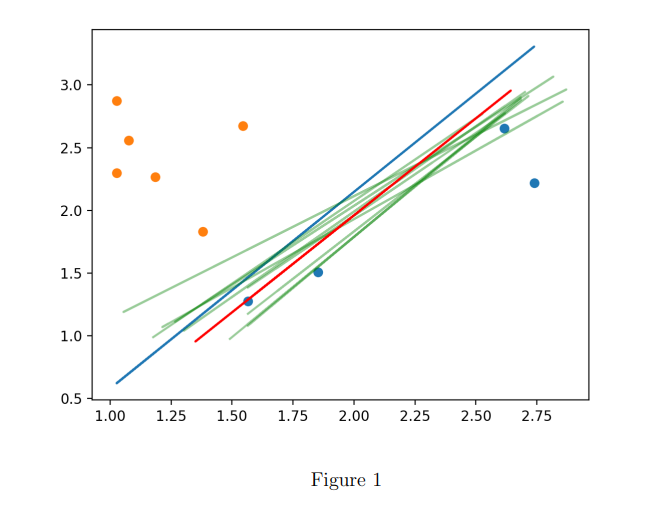
The passage discusses Figure 1, which illustrates the application of logistic regression in the author's algorithm. The true classifier is represented by y < 6ln(x), and the initial 10 samples are divided into two groups based on whether they meet the requirement or not. The blue line, generated by logistic regression, correctly classifies all 10 samples. The algorithm then samples 10 more points near the blue line, and all 20 points are used to update the classification line, resulting in green classification curves during iterations. The classification curve ultimately converges to the red line, with a classification accuracy of 67.4%. However, the low accuracy of logistic regression shows that it has some defects in non-linear classification problems, and improvements are needed to make it suitable for the author's algorithm.
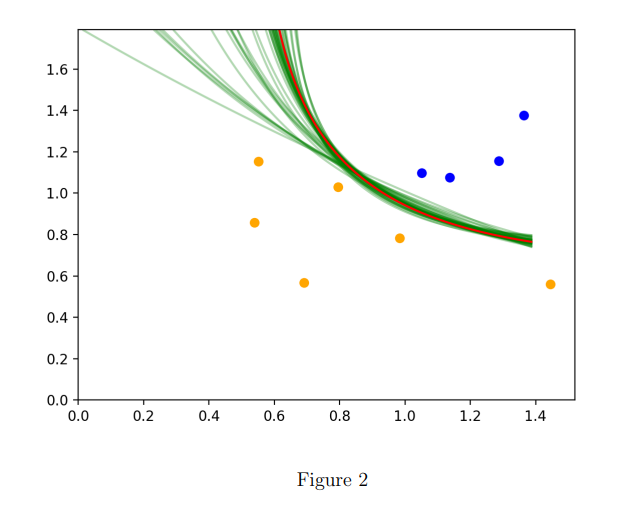
2.2 Kernel Logistic Regression:
The below image illustrates the result of the author's algorithm when applying the quadratic kernel in logistic regression, with the true classifier represented by xy > 1. The initial 10 samples are divided into two groups based on whether they meet the requirement or not. The first classification curve is linear, but as the number of iterations increases, the classification curve converges to the red line. The classification accuracy is 93.1%. Therefore, the author concludes that kernel logistic regression with the quadratic kernel is a suitable method for the algorithm in 2-dimensional cases.
3. Numerical case studies:
I have illustrated my algorithms in previous section. In the rest of report, I will implement the logistic regression with quadratic kernel in on numerical cases. In section 3.1, I will explain my construction of financial network based on the basic network model of Eisenberg and Noe (2001). Section 3.2 provides an analysis of the performance of my algorithm in a 2-bank system with plots. Section 3.3 summarizes the performance of my algorithm in high dimensions.
3.1 2-institution case:
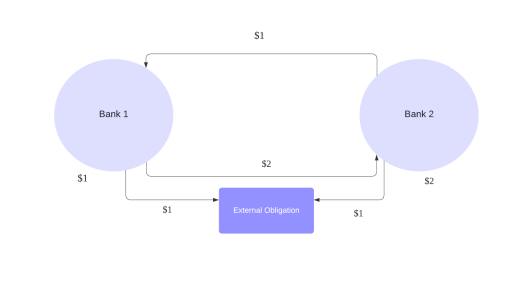
The scenario presented in this passage involves a system with two banks, where bank 1 initially has 1 dollar and bank 2 has 2 dollars. Bank 1 owes bank 2 1 dollar, and bank 2 owes bank 1 2 dollars. Both banks have an external obligation to pay 1 dollar. Given this information, bank 1 owes a total of 2 dollars, while bank 2 owes 3 dollars. Bank 1 must pay 1 dollar to bank 2, which represents a proportion of 1/2, while bank 2 must pay 2 dollars to bank 1, which represents a proportion of 2/3.
The below figure 4a shows the comparison of systemic risk measures approximated by my algorithm and the true boundary classified by grid search algorithm. My algorithm achieves a high accuracy and took about 32 minutes compared to 3 hours by grid search.
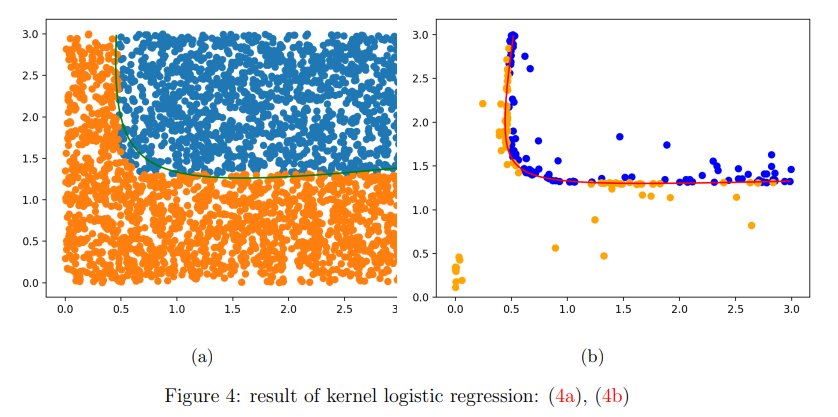
3.2 High dimensional cases:
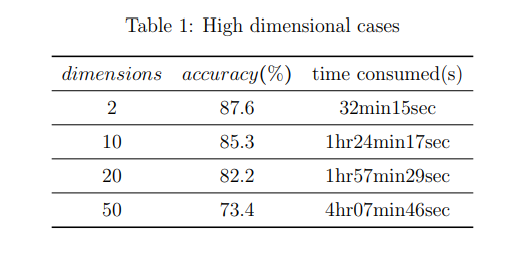
The below table shows the accuracy and running time of high dimensional cases. When dimension increased up to 50, my algorithm can always have a high accuracy which proves that kernel logistic regression is a valid method for computing high dimensional systemic risks.
Conclusion
The paper presents an algorithm that can efficiently compute high-dimensional systemic risks by using kernel logistic regression and a network model. Numerical cases demonstrate that the algorithm has a high level of accuracy and a relatively short running time.