Abstract
The Kalman Filter algorithm is an efficient methodology which has been wildly used in quantitative finance. It could be used to replicate financial data as funds or indexes and could also track historical parameters in the interest rate or volatility models. The success rate of the Kalman Filter model highly depends on the better estimation of both system and co-variance matrices. Also, most Kalman Filter study in portfolio replication have not taken the observation noise into account. We introduced the Double Sampling Kalman Filter algorithm based on the Forward-Backward Kalman Filter, demonstrated its capabilities in getting accurate portfolio weight estimations using only the prices of the portfolio and asset components.Its methodology and model validation are discussed. Its applications using real market data are discussed as well.
Research Topics:
Kalman Filter, Filtering, Portfolio replication, Portfolio reconstruction, Jump detection
Researchers:
Zimeng Cheng, Master in Financial Analytics, Graduated in Spring. 2019
Ou Hui, Master in Financial Engineering, Graduated in May. 2018
Zi Lang Wong, Master in Financial Engineering, Graduated in May. 2018
Qiaoqiao Zhang, Master in Financial Engineering, Graduated in May. 2018
Mu Tian, Master in Financial Engineering, Graduated in May. 2018
Advisor
Applications:
Although our ultimate goal is to reconstruct a hedge fund, we only want to show the capabilities of the DSKF algorithm using simpler systems. Obviously, index ETFs are easier to begin with. Firstly, Bloomberg provides daily weight data for index ETFs, which can be used as a known reference. Secondly, ETFs are similar to hedge funds but has less components in the asset universe. Lastly, the ETF price has higher data frequency than the hedge fund. Thus, we select the energy sector SPDR ETF XLE as our reconstruction target.
System Features:
Description of Double Sampling Kalman Filter
1. Apply the regular Kalman Filter in forward direction; Calculate the forward-sampling filter estimations for all time t.
2. Reverse the data direction: reverse time orders of the observations and the vector series; reverse time orders and inverse the model matrix; reverse time orders and flip the sign of the control vector (if any).
3. Assign the final estimation of the forward filter to the initial condition of the reverse filter; Apply the regular Kalman Filter to the reversed data; Calculate the reverse-sampling filter estimations for all time t.
4. Check whether the last estimation of the reverse-sampling filter is close to the initial condition of the forward-sampling filter
Main Results:
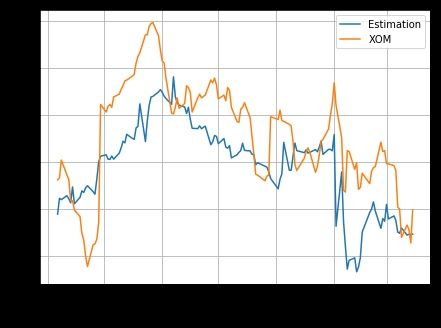
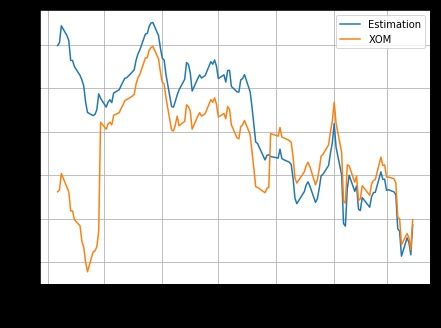
Conclusions:
The original Kalman Filter technique is a candidate tool for portfolio reconstructions. However, this method requires many input parameters that are difficult to determine in reality. In this case, we proposed the Double Sampling Kalman Filter (DSKF) algorithm, an advanced technique derived from the original Kalman Filter. It is designed to estimate the optimal filter parameters in order to further estimate the hidden portfolio weights. This technique is tested using the generated portfolios.
The algorithm is also applied to a real market portfolio, the energy sector SPDR ETF (XLE) with 32 asset components. The observed market price of the XLE ETF is always different to its net asset value (NAV) due to the market demand and supply.
Other aspects of the evaluation are carried out as well. The filter estimation results with respect to different data frequencies are studied. It is found that for this particular portfolio, the best data fetching interval is in the range of 15 ∼ 30 minutes.
From the results we conclude that the DSKF is a potential tool to reconstruct a financial portfolio. We believe that this technique is useful not only in portfolio reconstruction or replication, but also in many other engineering/financial areas. Its concept of utilizing the forward-sampling and backward-sampling Kalman Filters may be further applied to the Extended Kalman Filter and the particle filters in the future.